- Home
- Angry by Choice
- Catalogue of Organisms
- Chinleana
- Doc Madhattan
- Games with Words
- Genomics, Medicine, and Pseudoscience
- History of Geology
- Moss Plants and More
- Pleiotropy
- Plektix
- RRResearch
- Skeptic Wonder
- The Culture of Chemistry
- The Curious Wavefunction
- The Phytophactor
- The View from a Microbiologist
- Variety of Life
Field of Science
-
-
Change of address7 months ago in Variety of Life
-
Change of address7 months ago in Catalogue of Organisms
-
-
Earth Day: Pogo and our responsibility10 months ago in Doc Madhattan
-
What I Read 202411 months ago in Angry by Choice
-
I've moved to Substack. Come join me there.1 year ago in Genomics, Medicine, and Pseudoscience
-
-
-
-
Histological Evidence of Trauma in Dicynodont Tusks7 years ago in Chinleana
-
Posted: July 21, 2018 at 03:03PM7 years ago in Field Notes
-
Why doesn't all the GTA get taken up?7 years ago in RRResearch
-
-
Harnessing innate immunity to cure HIV9 years ago in Rule of 6ix
-
-
-
-
-
-
post doc job opportunity on ribosome biochemistry!11 years ago in Protein Evolution and Other Musings
-
Blogging Microbes- Communicating Microbiology to Netizens11 years ago in Memoirs of a Defective Brain
-
Re-Blog: June Was 6th Warmest Globally11 years ago in The View from a Microbiologist
-
-
-
The Lure of the Obscure? Guest Post by Frank Stahl13 years ago in Sex, Genes & Evolution
-
-
Lab Rat Moving House14 years ago in Life of a Lab Rat
-
Goodbye FoS, thanks for all the laughs14 years ago in Disease Prone
-
-
Slideshow of NASA's Stardust-NExT Mission Comet Tempel 1 Flyby15 years ago in The Large Picture Blog
-
in The Biology Files
Ode to a classic: The Nature of the Chemical Bond
New place, new view, slow reactions and the origins of life
I have been unable to blog for the past few days because I was busy moving to Chapel Hill for a postdoc at UNC Chapel Hill. I am very excited about this move and my upcoming research which is going to involve protein design and folding. Regular blogging will resume soon. Until then, happy holidays, and I will leave you with the following interesting paper published by a group from my new institution.
Stockbridge, R., Lewis, C., Yuan, Y., & Wolfenden, R. (2010). Impact of temperature on the time required for the establishment of primordial biochemistry, and for the evolution of enzymes Proceedings of the National Academy of Sciences, 107 (51), 22102-22105 DOI: 10.1073/pnas.1013647107
Making speculation official: More on the conservatism of leading science journals
Aliens, arsenic and alternative peer-review: Has science publishing become too conservative?
In 1959, physicists Philip Morrison and Giuseppe Cocconi advanced a hypothesis about how we could detect signals from extraterrestrial civilizations. The two suggested monitoring microwave signals from outer space at the frequency of 1420 MHz. This frequency is the frequency of neutral hydrogen, the most abundant element in the universe and one which aliens would likely harness for communication. The paper marked the beginning of serious interest in searching for extraterrestrial life. A year later, Freeman Dyson followed up on this suggestion with an even more fanciful idea. He conjectured that a sufficiently advanced civilization might be able to actually disassemble a planet the size of Jupiter and use its parts to create a shell of material that would surround the parent planet’s solar system. This sphere would capture solar energy and allow civilizations to make the most efficient use of all such energy. The most telling signature of such an advanced habitat would be an intense infrared signal coming from the sphere. Thus Dyson recommended looking for infrared signals in addition to radio signals if we were to search for aliens. The sphere came to be known as a ‘Dyson sphere’ and became fodder for a generation of science fiction enthusiasts and Star Trek fans.
These two ideas and especially the second one sound outrageous and highly speculative to say the least. Can you guess where both were published? In the two most prestigious science journals in the world; the Morrison paper was published in Nature while Dyson published his report in Science. This was in 1960. I can say in a heartbeat that I don’t see similar ideas being published in these journals today, and this is a situation which we all should regret.
I bring up this issue because I think it indicates the significant changes in attitude about publishing novel scientific ideas that have occurred from 1960 to the present. In 1960 even serious journals like Nature and Science were open to publishing fanciful speculation, provided it was clearly enumerated. Now the demands for publishing have become more stringent, but also more narrowly defined. While this may have led to the publishing of more ‘concrete’ science, it has also dissuaded researchers from venturing out into novel territory. Most importantly, it has led the scientific community to put an unnecessarily high premium on ideas being right rather than interesting.
Science progresses not by being right or wrong but by being interesting. Most scientific ideas in their infancy are tentative, unsubstantiated and incomplete. Yet modern scientific publishing and peer review largely discourage the presentation of these ideas by insisting on convincing evidence that they are right. In most cases this emphasis on accuracy and complete validation is necessary to save science from itself; we have seen all too many cases of pseudoscience that looked superficially plausible but which turned out to be full of holes. Science usually plays it safe by insisting on unimpeachable evidence. But in my opinion this stringent self-correcting process has gone too far, and in our desire to err on the safer side we have erred on the extreme side. This is having a negative impact on what we can call creative science. The insistence on foolproof data and the public censure that researchers would face if they don’t provide it is deterring many scientists from publishing provocative results that are still in the early stages of gestation. Demands for conservative presentation are also accompanied by conservative peer review since reviewers fear backlash as much as authors. All this is unfortunate and is to the detriment of the very core of scientific progress, since it’s only when provocative ideas are published can other researchers validate, verify and refute them.
The furor about the recent paper on “arsenic-based” life brings these issues into sharp focus. Much of the hailstorm of criticism would have been avoided if the standards and formats of scientific publishing allowed the presentation of ideas that may not be fully substantiated but which are nonetheless interesting. By now we are all familiar with the torrent of criticism about the paper that has come from all quarters, from blog posts to opinions from well-known experts. What is clear is that the experiments done were shoddy and controls were lacking. But the criticism is detracting from the potential value of the paper. Irrespective of whether the claims of arsenic actually being incorporated in the bacterium’s replicative and metabolic machinery are true, the paper is undoubtedly interesting, if only as an example of a hitherto unknown novel extremophile. Yet it is in danger of simply being forgotten as one of the uglier episodes in the history of science publishing.
There is in fact a solution to this problem, one which I have been in favor of for a long time. What if there was a separate section specifically devoted to relatively far-fetched ideas and this paper had been published in that section? The paper would then likely have been taken much less seriously and its tenets would have been accepted simply as thought-provoking observations pointing to further experimentation rather than established facts. So here’s my suggestion; let the top scientific journals have a separate section entitled ‘Speculation’ (or perhaps ‘Imaginings’) which allows the presentation of ideas that are fanciful and speculative. The ideas proposed could range from purely theoretical constructs to the documentation and interpretation of unusual experimental observations. The only requirement is that they should be unorthodox and interesting, backed up by more or less known scientific principles, clearly defined and enumerated and contain testable hypotheses. Let there be a second type of peer-review process for these ideas, one which is as honest as the primary process but more forgiving of the lack of foolproof evidence.
The idea about Dyson spheres would fit in nicely in such a section. Another example that comes to my mind is an idea proposed by the biophysicist Luca Turin. Turin conjectured that we may smell molecules based not on their shape but on the vibrations of their bonds. The history of this idea is interesting since others had already proposed it earlier in respectable journals. Turin actually wrote it up and sent it to Nature. Nature deliberated for an entire year and rejected the paper. In this case Nature should at least be commended for taking so long and presumably giving careful consideration to the idea, but the point is that they wouldn’t have had a problem publishing it in a ‘Speculation’ section right away. Turin’s idea was interesting, novel, highly interdisciplinary, enumerated in great detail and backed up by well-known principles of chemistry and spectroscopy. It satisfied all the criteria of a novel scientific idea that may or may not be right. Turin finally published in a journal which only specialists read, thus precluding the concept from being appreciated by an interdisciplinary cross-section of scientists. There is now at least some evidence that his ideas may be right.
Interestingly, there is at least one entire journal devoted to the publication of interesting hypotheses. This is the journal ‘Medical Hypotheses’. Medical Hypotheses prominently lacks peer review (although they have instituted some peer review recently) and has occasionally come under fire for publishing highly questionable papers, such as those criticizing the link between HIV and AIDS. But it has also served as a playground for the interaction of many interesting ideas. The editorial board of Medical Hypotheses features highly respected scientists like the neurologist V S Ramachandran and the Nobel Prize winning neuroscientist Arvid Carlsson. Ramachandran himself has iterated the need for such a journal. Science and Nature merely have to devote a small section in each issue to the kinds of ideas that are published in Medical Hypotheses, perhaps with a higher standard.
It’s worth reiterating Thomas Kuhn’s notions of paradigm shifts in science here. Scientific paradigms rarely change by playing it safe. Most scientific revolutions have been initiated by bold and heretical ideas from maverick individuals, whether it was Darwin’s ideas about natural selection, Einstein’s thoughts about the constancy of the speed of light, Wegener’s ideas about continental shift or Bohr’s construction of the quantum atom. Not a single one of these ideas was validated by foolproof evidence when it was proposed. Many of them sounded outright bizarre and counter-intuitive. But it was still paramount to bring these ideas to a greater audience. Only time would tell whether they were right or wrong, but they were undoubtedly supremely novel and interesting. And almost all of them were published by leading journals. It was the willingness to entertain interesting ideas that made possible the scientific revolutions of the twentieth century. It seems to be a strange historical anomaly to find journals much more prone to publishing speculative ideas a hundred years ago than today. Today we seem to worship the safety of truth at the expense of the uncertain but bold reaches of novelty.
Of course, the existence of a second-tier of publication and peer review would undoubtedly have to be carefully monitored. There is after all a thin line between reasonable speculation and pseudoscience. The reviewers in this tier would have to pay even more careful attention than they usually do to ensure that they are not pushing baseless fantasies. But as we have seen in the case of the vibrational theory of smell and the case of arsenic-loving bacteria, it’s not that hard to separate legitimate science with uncertain truth value from mere storytelling.
Once the ground rules are established and the initial obstacles are overcome, the second tier of peer review would have many advantages apart from encouraging the publication of speculation. It would also make reviewers more comfortable in recommending publication; since the ideas are speculative anyway, they would not insist on complete verification and would not fear backlash if the ideas they had reviewed turn out to be wrong. Journal editors would similarly find it easier to approve publication. And the scientific community at large perhaps would not be as critical as it has been in the case of the recent paper because it too would accept the proposed ideas not as declarations of truth but as tentative exploration. But the greatest beneficiaries of the improved system would undoubtedly be the publishing scientists. Their minds would be much freer to dream and they would fear much less retaliation from the community for daring to do this. Most importantly, unlike the recent case, they would not be under pressure to make statements whose implications exceed the objective factual implications of their claims, and they would be happy to just present the claims as interesting observations that point the way towards further experiments.
Science progresses by being the ultimate free-market of ideas; this has led to it being a highly social process where scientists build on each other’s work. But for this social process to work the ideas must be liberated from their initial nebulous beginnings. Ideas in the scientific marketplace come in different flavors, from boring and established to interesting and maverick. The current scientific publication and peer-review process imposes a straitjacket that ideas have to fit in in order to be ‘pre-selected’ for entry into this market. This keeps out some of the most interesting ideas and more importantly, dissuades thinkers from even pursuing them in the first place. The straitjacket does serve the valuable purpose of filtering flotsam but it is also filtering out too many other interesting things. Science is too haphazard and full of unexpected twists and turns to be entrusted to rigid rules of review and publication. We need to accept the liability of occasionally having a dubious idea published in order to keep open the possibility of also giving novel beginnings a public platform; the beauty of science is that the bonafide dubious ideas automatically get weeded out through scrutiny and so we should not have to worry about too many of them going on extended rampages. But the potentially good ideas can only be fleshed out by other scientists when they are allowed to be exposed to criticism, appreciation and ridicule. Even if the ideas themselves ultimately sink, they may serve as spores which lead to the germination of other ideas. And it is the germination of these other ideas that gets transformed into trees of scientific discovery.
We are all sheltered, invigorated and inspired by the branches of these trees. Let’s give them an opportunity to grow.
An eternity of infinities: the power and beauty of mathematics
Gamow starts by alerting us to the Hottentot tribe in Africa. Members of this tribe cannot formally count beyond three. How then do they compare commodities such as animals whose numbers are greater than three? By employing one of the most logical and primitive methods of counting- the method of counting by one-to-one correspondences or put more simply, by pairing objects with each other. So if a Hottentot has ten animals and she wishes to compare these with animals from a rival tribe, she will pair off each animal with its counterpart. If animals are left over in her own collection, she wins. If they are left over in her rival’s collection, she has to admit the rival tribe’s superiority in sheep.
What is remarkable is that this simplest of counting methods allowed the great German mathematician Georg Cantor to discover one of the most stunning and counter-intuitive facts ever divined by pure thinking. Consider the set of natural numbers 1, 2, 3… Now consider the set of even numbers 2, 4, 6…If asked which set is greater, commonsense would quickly point to the former. After all the set of natural numbers contains both even and odd numbers and this would of course be greater than just the set of even numbers, wouldn’t it? But if modern science and mathematics have revealed one thing about the universe, it’s that the universe often makes commonsense stand on its head. And so it is the case here. Let’s use the Hottentot method. Line up the natural numbers and the even numbers next to each other and pair them up.
1 2 3 4 5…
2 4 6 8 10…
So 1 pairs up with 2, 2 pairs up with 4, 3 pairs up with 6 and so on. It’s now obvious that every natural number n will always pair up with an even number 2n. Thus the set of natural numbers is equal to the set of even numbers, a conclusion that seems to fly in the face of commonsense and shatters its visage. We can extend this conclusion even further. For instance consider the set of squares of natural numbers, a set that would seem even ‘smaller’ than the set of even numbers. By similar pairings we can show that every natural number n can be paired with its square n2, again demonstrating the equality of the two sets. Now you can play around with this method and establish all kinds of equalities, for instance that of whole numbers (all positive and negative numbers) with squares.
But what Cantor did with this technique was much deeper than amusing pairings. The set of natural numbers is infinite. The set of even numbers is also infinite. Yet they can be compared. Cantor showed that two infinities can actually be compared and can be shown to be equal to each other. Before Cantor infinity was just a place card for ‘unlimited’, a vague notion that exceeded man’s imagination to visualize. But Cantor showed that infinity can be mathematically precisely quantified, captured in simple notation and expressed more or less like a finite number. In fact he found a precise mapping technique with which a certain kind of infinity can be defined. By Cantor’s definition, any infinite set of objects which has a one-to-one mapping or correspondence with the natural numbers is called a ‘countably’ infinite set of objects. The correspondence needs to be strictly one-to-one and it needs to be exhaustive, that is, for every object in the first set there must be a corresponding object in the second one. The set of natural numbers is thus a ruler with which to measure the ‘size’ of other infinite sets. This countable infinity was quantified by a measure called the ‘cardinality’ of the set. The cardinality of the set of natural numbers and all others which are equivalent to it through one-to-one mappings is called ‘aleph-naught’, denoted by the symbol
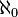 . The set of natural numbers and the set of odd and even numbers constitute the ‘smallest’ infinity and they all have a cardinality of
. The set of natural numbers and the set of odd and even numbers constitute the ‘smallest’ infinity and they all have a cardinality of 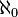 . Sets which seemed disparately different in size could all now be declared equivalent to each other and pared down to a single classification. This was a towering achievement.
. Sets which seemed disparately different in size could all now be declared equivalent to each other and pared down to a single classification. This was a towering achievement.The perplexities of Cantor’s infinities led the great mathematician David Hilbert to propose an amusing situation called ‘Hilbert’s Hotel’. Let’s say you are on a long journey and, weary and hungry, you come to a fine-looking hotel. The hotel looks like any other but there’s a catch: much to your delight, it contains a countably infinite number of rooms. So now when the manager at the front desk says “Sorry, but we are full”, you have a response ready for him. You simply tell him to move the first guest into the second room, the second guest into the third room and so on, with the nth guest moving into the (n+1)th room. Easy! But now what if you are accompanied by your friends? In fact, what if you are so popular that you are accompanied by a countably infinite number of friends? No problem! You simply ask the manager to move the first guest into the second room, the second guest into the fourth room, the third guest into the sixth room…and the nth guest into the 2nth room. Now all the odd-numbered rooms are empty, and since we already know that the set of odd numbers is countably infinite, these rooms will easily accommodate all your countably infinite guests, making you even more popular. Mathematics can bend the laws of the material world like nothing else.
But the previous discussion leaves a nagging question. Since all our infinities are countably infinite, is there something like an ‘uncountably’ infinite set? In fact, what would such an infinity even look like? The ensuing discussion probably constitutes the gem in the crown of infinities and it struck infinite wonder in my heart when I read it.Let’s consider the set of real numbers, numbers defined with a decimal point as a.bcdefg... The real numbers consist of the rational and the irrational numbers. Is this set countably infinite? By Cantor’s definition, to demonstrate this we would have to prove that there is a one-to-one mapping between the set of real numbers and the set of natural numbers. Is this possible? Well, let’s say we have an endless list of rational numbers, for instance 2.823, 7.298, 4.001 etc. Now pair up each one of these with the natural numbers 1, 2, 3…, in this case simply by counting them. For instance:
S1 = 2.823
S2 = 7.298
S3 = 4.001
S4 = …
Have we proved that the rational numbers are countably infinite? Not really. This is because I can construct a new real number not on the list using the following prescription: construct a new real number such that it differs from the first real number in the first decimal place, the second real number in the second decimal place, the third real number in the third decimal place…and the nth real number in the nth decimal place. So for the example of three numbers above the new number can be:
S0 = 3.942
(9 is different from 8 in S1, 4 is different from 9 in S2 and 2 is different from 1 in S3)
Cantor called this argument the ‘diagonal argument’ since it really constructs a new real number from a line that’s diagonally drawn across all the relevant numbers after the decimal points in each of the listed numbers. The image from the Wikipedia page makes the picture clearer:

In this picture, the new number is constructed from the red numbers on the diagonal. It’s obvious that the new number Eu will be different from every single number E1…En on the list. The diagonal argument is an astonishingly simple and elegant technique that can be used to prove a deep truth.
With this comparison Cantor achieved something awe-inspiring. He showed that one infinity can be greater than another, and in fact it can be infinitely greater than another. This really drives the nail in the coffin of commonsense, since a ‘comparison of two infinities’ appears absurd to the uninformed mind. But our intuitive ideas about sets break down in the face of infinity. A similar argument can demonstrate that while the rational numbers are countably infinite, the irrational numbers are uncountably so. This leads to another shattering comparison; it tells us that the tiny line segment between 0 and 1 on the number line containing real numbers (denoted by [0, 1]) is ‘larger’ than the entire set of natural numbers. A more spectacular case of David obliterating Goliath I have never seen.
The uncountably infinite set of reals comprises a separate cardinality from the cardinality of countably infinite objects like the naturals which was denoted by
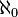 . Thus one might logically expect the cardinality of the reals to be denoted by ‘
. Thus one might logically expect the cardinality of the reals to be denoted by ‘ ’. But as usual reality thwarts logic. This cardinality is actually denoted by ‘c’ and not by the expected
’. But as usual reality thwarts logic. This cardinality is actually denoted by ‘c’ and not by the expected  . Why this is so is beyond my capability to understand, but it is fascinating. While it can be proven that 2^
. Why this is so is beyond my capability to understand, but it is fascinating. While it can be proven that 2^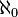 = c,the hypothesis that c =
= c,the hypothesis that c =  is actually just a hypothesis, not a proven and obvious fact of mathematics. This hypothesis is called the ‘continuum hypothesis’ and happens to be one of the biggest unsolved problems in pure mathematics. The problem was in fact the first of the 23 famous problems for the new century proposed by David Hilbert in 1900 during the International Mathematical Congress in France (among others on the list were the notorious Riemann hypothesis and the fond belief that the axioms of arithmetic are consistent, later demolished by Kurt Gödel). The brilliant English mathematician G H Hardy put the continuum at the top of his list of things to do before he died (he did not succeed). A corollary of the hypothesis is that there are no sets with cardinality between
is actually just a hypothesis, not a proven and obvious fact of mathematics. This hypothesis is called the ‘continuum hypothesis’ and happens to be one of the biggest unsolved problems in pure mathematics. The problem was in fact the first of the 23 famous problems for the new century proposed by David Hilbert in 1900 during the International Mathematical Congress in France (among others on the list were the notorious Riemann hypothesis and the fond belief that the axioms of arithmetic are consistent, later demolished by Kurt Gödel). The brilliant English mathematician G H Hardy put the continuum at the top of his list of things to do before he died (he did not succeed). A corollary of the hypothesis is that there are no sets with cardinality between 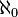 and c. Unfortunately the continuum hypothesis may be forever beyond our reach. The same Gödel and the Princeton mathematician Paul Cohen damned the hypothesis by proving that, assuming the consistency of the basic foundation of set theory, the continuum hypothesis is undecidable and therefore it cannot be proved nor disproved. This is assuming that there are no contradictions in the basic foundation of set theory, something that itself is 'widely believed' but not proven. Of course all this is meat and drink for mathematicians wandering around in the most abstract reaches of thought and it will undoubtedly keep them busy for years.
and c. Unfortunately the continuum hypothesis may be forever beyond our reach. The same Gödel and the Princeton mathematician Paul Cohen damned the hypothesis by proving that, assuming the consistency of the basic foundation of set theory, the continuum hypothesis is undecidable and therefore it cannot be proved nor disproved. This is assuming that there are no contradictions in the basic foundation of set theory, something that itself is 'widely believed' but not proven. Of course all this is meat and drink for mathematicians wandering around in the most abstract reaches of thought and it will undoubtedly keep them busy for years.But it all starts with the Hottentots, Cantor and the most primitive methods of counting and comparison. I happened to chance upon Gamow’s little gem yesterday, and all this came back to me in a rush. The comparison of infinities is simple to understand and is a fantastic device for introducing children to the wonders of mathematics. It drives home the essential weirdness of the mathematical universe and raises penetrating questions not only about the nature of this universe but about the nature of the human mind that can comprehend it. One of the biggest questions concerns the nature of reality itself. Physics has also revealed counter-intuitive truths about the universe like the curvature of space-time, the duality of waves and particles and the spooky phenomenon of entanglement, but these truths undoubtedly have a real existence as observed through exhaustive experimentation. But what do the bizarre truths revealed by mathematics actually mean? Unlike the truths of physics they can’t exactly be touched and seen. Can some of these such as the perceived differences between two kinds of infinities simply be a function of human perception, or do these truths point to an objective reality ‘out there’? If they are only a function of human perception, what is it exactly in the structure of the brain that makes such wondrous creations possible? In the twenty-first century when neuroscience promises to reveal more of the brain than was ever possible, the investigation of mathematical understanding could prove to be profoundly significant.
Blake was probably not thinking about the continuum hypothesis when he wrote the following lines:
To see a world in a grain of sand,
And a heaven in a wild flower,
Hold infinity in the palm of your hand,
And eternity in an hour.
But mathematics would have validated his thoughts. It is through mathematics that we can hold not one but an infinity of infinities in the palm of our hand, for all of eternity.
Medicine! Poison! Arsenic! Life itself!
A few months back when the Nobel Prize for chemistry was announced, a few observers lamented that unlike physics and biology, perhaps chemistry does not have any 'big' questions to answer. So here's a question for these skeptics. What branch of science has the biggest bearing on the discovery of an organism that utilizes arsenic instead of phosphorus? If you say "biology" or "geology" you would be wrong. The essential explanation underlying today's headline about an arsenic-guzzling bacterium is at the chemical level. The real question to ask is about the key molecular mechanisms in which arsenic substitutes phosphorus. What molecular level events enable this novel organism to survive, metabolize and reproduce? Of course the discovery is significant for all kinds of scientists including biologists, geologists, astronomers and perhaps even philosophers, but the essential unraveling of the puzzle will undoubtedly be at the level of the molecule.
Many years back I read a classic paper by the late Harvard chemist Frank Westheimer called "Why Nature Chose Phosphates". In simple and elegant terms, Westheimer explained why arsenic cannot replace phosphorus and silicon cannot replace carbon in the basic chemistry of life. In a nutshell, phosphates have the right kind of acid-base behavior at physiological pH. The single negative charge in phosphates in DNA hinders nucleophilic attack by water and hydrolysis without making the system so stable that it loses its dynamic nature. Arsenates, simply put, are too unstable. So are silicates.
And yet we have an arsenate-metabolizing bacterium here. Arsenic, the same stuff that was used in outrageous amounts in Middle-Age medicines and which later turned into the diabolical murderer's patent weapon of choice makes a new appearance now as a sustainer of life. First of all let's be clear on what this is not. It's not an indication that "life arose twice", it does not suddenly promise penetrating insight into extraterrestrial life, it probably won't win its discoverers a Nobel Prize and in fact it's not even technically speaking an 'arsenic-based life form'. The bacteria were found in a highly saline and alkaline lake with a relatively high concentration of arsenic where they were happily using conventional phosphorus-based chemistry. The fun started when they were gradually exposed to increasing concentrations of arsenic and increasing dilutions of phosphorus. The hardy little creatures still continued to grow.
But the real surprise was when the cellular components were analyzed and found to contain a lot of arsenic and very little phosphorus, certainly too less to sustain the metabolic machinery of life. If true this is a significant discovery, although not too surprising. Chemistry deals with improbabilities, not impossibilities. Life forms utilizing arsenates were conjectured to exist for some time, but such total substitution of arsenic for phosphorus was not anticipated.
If validated the work raises fascinating questions, not about extraterrestrial life or even about life's origins, but more mundane and yet probing ones about the basic chemistry of life. I haven't read the original paper in detail yet, but here are a few thoughts whose confirmation would lead to new territory:
1. The best thing would be to get a crystal structure of arsenic-based DNA. That would be a slam dunk and would really catapult the discovery to the front ranks of novelty. The second-best thing would be to do experiments involving labeled phosphorus and arsenic, to find out the exact proportion of arsenic getting incorporated. Which brings us to the next point.
2. How much of the cellular components are trading phosphorus for arsenic? Life's molecules are crucially dependent on phosphate. Not just DNA but signaling molecules like kinases and AMP are phosphorus-based. And of course there's ATP. What is fascinating to ponder is whether all of these key molecules traded phosphorus for arsenic. Perhaps some of them like DNA are using arsenic while others keep on using phosphorus. Checking the numbers and concentrations left over would certainly help to decide this.
One thing that should be confirmed and re-confirmed beyond the slightest shade of doubt is that there is absolutely no phosphorus hanging around which would be sufficient to sustain basic life processes; the entire conclusion depends on this fact. Traces of phosphorus can come from virtually anywhere; from the media (no, not the journalists, although it could come from them too), from human bodies, from laboratory equipment. A rough analogy from chemistry comes to mind; we have seen in the past how 'transition metal-free' reactions turned out to be catalyzed by traces of transition metals. If life is pushed to the brink by decreasing the phosphorus levels in its environment, the first thing we would expect it to do would not be to use arsenic but to scavenge the tiniest amounts of vital phosphorus from its environment with fanatic efficiency. It's interesting to note that the phosphorus concentrations being measured are in femtograms, which means that the error bars need to be zealously monitored. If it turns out that there is enough phosphorus to sustain a core cycle of essential processes while others are utilizing arsenic, the conclusions drawn would still be interesting but not as revolutionary as the current ones, and we probably won't be calling it an 'arsenic-based' life form then. In any case, my guess is that the utilization of phosphorus was selective and not ubiquitous. Organisms rarely utilize all-or-none principles and usually do their best under the circumstances.
If arsenic is truly substituting phosphorus in all these signaling, genetic and structural components, that would really be something because it would create more questions. By what pathways does arsenic enter these molecules? How does it affect the kinetics of reactions involving them? And most important are questions about molecular recognition. There are hundreds of proteins that recognize phosphorylated protein residues and similar other molecules. Do all these proteins recognize their arsenic containing counterparts? If so, is this the result of mutations in most of these proteins?; it seems hard to imagine that simultaneous mutations in so many biomolecules to make them recognize arsenic would result in viable living organisms. A more conservative explanation is that most of these molecules don't mutate but still recognize arsenic, albeit with different specificities and affinities that are nonetheless feasible for keeping life's engine chugging. The molecules of life are exquisitely specific but they are also flexible and amenable to changing circumstances. They have to be so.
3. And finally of course, how does the protein expression systems of the bacteria cope with arsenic-based DNA? As mentioned above, arsenates are unstable. To counter this instability does DNA expression simply get ramped up? How do proteins control the unpacking, packing, duplication and transcription of this unusual form of DNA? For starters, how does DNA polymerase zip together arsenated nucleotides for instance? How does the whole thing essentially hold together?
There are of course more questions. Whatever the implications, this is an interesting discovery that would keep scientists busy for a long time. Like all truly interesting scientific discoveries it asks more questions than it answers. But ultimately it should come as no surprise. The wonders of chemistry combined with those of Darwinian evolution have allowed life to conquer unbelievably diverse niches, from methane-riddled environments to hot springs to sub-zero temperatures. In one way this discovery would only add one more feather into the cap of a robust and abiding belief- that life is tough. It survives.
Selenium for sulfur should be next (but I wouldn't wait around for silicon...)
Wolfe-Simon, F., Blum, J., Kulp, T., Gordon, G., Hoeft, S., Pett-Ridge, J., Stolz, J., Webb, S., Weber, P., Davies, P., Anbar, A., & Oremland, R. (2010). A Bacterium That Can Grow by Using Arsenic Instead of Phosphorus Science DOI: 10.1126/science.1197258
Probing amyloid, one oligomer at a time
One of the more important paradigm shifts in our understanding of the Alzheimer’s disease-causing amyloid protein in the last few years has been the recognition of differences between the well known polymer aggregates of amyloid and their smaller, soluble oligomer counterparts. For a long time it was believed that the fully formed 40-42 amino acid protein aggregate found in autopsies was the causative agent in AD, or at least the most toxic one. This understanding has radically changed in the last few years, partly through elegant work done in identifying oligomers and partly through the unfortunate results of clinical trials targeting amyloid. The new understanding is that it’s not the fully formed aggregates but the smaller oligomers that are the real toxic species.
Identifying these different monomers, dimers, trimers and tetramers is a valuable goal. But until now their recognition has mainly depended on raising specific antibodies against them, a tedious and expensive process. Small molecule probes that specifically identify each oligomer have been missing. In a recent JACS communication, a team from the University of Michigan uses a simple but clever technique to develop such probes and makes a promising step in this direction.
The probes are based on the idea that the best antidote against a poison is another poison. In this case the poison is the specific sequence of amino acids that makes up amyloid. In particular, a sequence of five amino acids- KLVFF- has been found to be sufficient for aggregation and toxicity. The aggregates form by the stacking of beta sheets principally driven by hydrophobic interaction between the FF residues; each pair thus serves as a growth site for addition of further such residues. The insight then is that if one could construct a mimic of the sequence, this mimic would basically act as a competitive inhibitor and bind to the normal sequence, inhibiting further growth. In this case the strategy was to use KLVFF segments themselves which would sort of wrap around newly formed oligomers of different constitution and sequester them from further self-assembly. So the team essentially constructed two KLVFF segments joined by a linker. The linker would also serve the purpose of providing an entropic advantage to the two segments so that they would not be at an energetic disadvantage during binding. The important question was how long the linker should be.
To decide on the length of the linker the team made some clever use of molecular dynamics simulations. Since you can estimate the approximate thickness of every oligomer, you can estimate the linker length that would be required to keep two KLVFF segments at the same distance as the thickness of the oligomer. For instance, the distances between the segments needed to wrap around the oligomers were 14-15 A for the dimer, 19-20 A for the trimer and 24-25 A for the tetramer.

But the linker should also keep the segments stable at that distance. To probe this the team used MD simulations. The MD simulations revealed the length of the linker required to keep the two segments separated at the specific distances by indicating how much time the assembly spent at those distances.
To test these results, the team then generated mixtures of different kinds of KLVFF oligomers and then added each probe to the solution. A streptavidin moiety was attached to every probe. Silver staining revealed that each probe was specifically binding to an oligomer of a certain type dictated by the compatibility of the intraprobe distance and oligomer thickness. Trimers and tetramers could be clearly identified but there was more ambiguity in case of dimers, presumably because of their less ordered structure.
Most interestingly, the team then added the probes to cerebrospinal fluid (CSF). Since amyloid is part of normal physiology, it is present in CSF. Gratifyingly they found that the probes could very clearly label trimers and tetramers against a background of several other proteins and intermediates in CSF. This experiment notably demonstrates that the method can selectively detect amyloid oligomers in complex mixtures.
I think that this work is valuable and paves the way toward the development of similar small-molecule based probes for identifying the key intermediates in amyloid formation. It could also be very useful in exploring amyloid formation in normal physiology and in exploring the stages of protein self-assembly in diverse amyloid-based diseases.
Reinke, A., Ung, P., Quintero, J., Carlson, H., & Gestwicki, J. (2010). Chemical Probes That Selectively Recognize the Earliest Aβ Oligomers in Complex Mixtures Journal of the American Chemical Society DOI: 10.1021/ja106291e
















