Richard L. Garwin (1928-2025): Force of Nature

There are physicists, and then there are physicists. There are engineers, and then there are engineers. There are government advisors, and then there are government advisors.

And then there’s Dick Garwin.

Richard L. Garwin, who his friends and colleagues called Dick, has died at the age of 97. He was a man whose soul imbibed technical brilliance and whose life threaded the narrow corridor between Promethean power and principled restraint. A scientist of prodigious intellect and unyielding moral seriousness, his career spanned the detonations of the Cold War and the dimming of the Enlightenment spirit in American public life. He was, without fanfare or affectation, the quintessential citizen‑scientist—at once a master of equations and a steward of consequence. When you needed objective scientific advice on virtually any technological or defense‑related question, you asked Dick Garwin, even when you did not like the advice. Especially when you did not like it. And yet he was described as “the most influential scientist you have never heard of”, legendary in the world of physics and national security but virtually unknown outside it.

He was born in Cleveland in 1928 to Jewish immigrants from Eastern Europe, and quickly distinguished himself as a student whose mind moved with the inexorable clarity of first principles. His father was an electronics technician and high school science teacher who moonlighted as a movie projectionist. As a young child Garwin was already taking things apart, with the promise of reassembling them. By the age of 21 he had earned his Ph.D. under Enrico Fermi, who—legend has it—once remarked that Garwin was the only true genius he had ever met. This was not idle flattery. After Fermi, Dick Garwin might be the closest thing we have had to a universal scientist who understood the applied workings of every branch of physics and technology. There was no system whose principles he did not comprehend, whether mechanical, electrical or thermodynamic, no machine that he could not fix, no calculation that fazed him. Just two years after getting his Ph.D., Garwin would design the first working hydrogen bomb, a device of unprecedented and appalling potency, whose test, dubbed “Ivy Mike,” would usher in a new and even graver chapter of the nuclear age.

Yet Garwin was never intoxicated by power. Because he thought the creation of the hydrogen bomb was driven by the exigencies of the age, he did not regret his work, but neither did he revel in it, seeking instead to control its worst excesses. For decades his contribution remained unknown, and he never bothered to update the record, saying that he could either get something done or get credit for it, but not both. Unlike many of his contemporaries, who leapt eagerly into the vortex of Cold War prestige and developed the braggadocio to go along with it, Garwin remained a paradoxical figure: at once the architect of supreme destructive force and one of its most persistent critics. He understood—perhaps more than any other scientist of his generation—that technical brilliance without ethical deliberation is merely efficiency in the service of catastrophe. He understood that his main job was to shoot down boondoggles and billion‑dollar bad ideas which were a defense department specialty. As perhaps the best example of how he saw his main function as offering stone‑cold sober advice based on the best technical analysis, he along with Hans Bethe pointed out fatal flaws with the Johnson administration’s ABM system and the Reagan administration’s SDI (Strategic Defense Initiative, derisively called Star Wars) system. As a member of Nixon’s science advisory council, he killed the proposal for a supersonic jetliner after citing noise pollution and structural concerns. In return the vindictive Nixon killed the science advisory council.

Garwin would advise every president from Truman to Obama, Republican and Democrat alike, offering a rare and vanishing example of a mind that could not be bought, flattered, or ideologically corralled. George W. Bush awarded him the National Medal of Science; Obama the nation’s highest civilian honor, the Presidential Medal of Freedom. He advised Kennedy during the Cuban Missile Crisis, pushed for the Anti‑Ballistic Missile Treaty under Nixon, helped Obama deal with the Deep Horizon Oil Spill and warned, presciently, of the folly of weaponizing space. From submarines to space weapons, from missile defense to nuclear disarmament, from oil spills to solar power, there was no field in which Garwin was not an expert, often the preeminent expert. Long after his hydrogen bomb design became a grim historical footnote, his advocacy for arms control, transparency, and rational defense policy continued unabated—earnest, unfashionable, and, above all, indispensable. As the physicist Freeman Dyson who was one of his fellow technical experts put it, Garwin was a prime example of how one man with a backpack could beat an army of government bureaucrats, if only that man’s name was Dick Garwin.

But to speak only of his role in the nuclear age is to risk caricature. Garwin’s genius was dazzlingly catholic. His parallel career at IBM mirrored some of the great technological innovations of our modern age. IBM prized him so highly that they allowed him to spend a third of his time doing classified government work on their dime. And their astute hiring decision paid off in spades. Garwin’s fingerprints are found in the design of gravitational wave detectors, in the refinement of MRI technology, in the development of GPS and satellite reconnaissance systems. He contributed to the understanding of superconductivity, to the design of the compact disc and the touch screen, to cryptography and to high‑energy physics – he narrowly missed the Nobel Prize for an experiment he conducted in his 20s to demonstrate what’s called parity violation in beta decay. And he did all this with a kind of quiet, omnidirectional intensity that shunned limelight but advanced civilization in tangible ways.

Garwin authored over 500 scientific papers, many of them marked not just by precision but by restraint—proposing solutions rather than pronouncements, elevating fact over flourish. He felt it his public responsibility to put almost the entire corpus of his unclassified work online at the Garwin Archive – more than 1600 pages of presentations, talks and technical analysis covering almost every defense‑related topic. If the academy in recent decades has become a theater of self‑display, Garwin belonged to an older order: one in which brilliance did not demand amplification, and integrity required no branding. As he said in a documentary made about him a few years ago, the preservation of our democracy was his lodestar; nothing else mattered if that goal could not be achieved.

Garwin kept on working, traveling, advising, relentlessly, until almost his last day. When he was 88 I had the privilege of having an email exchange with him about a project I was working on. My one‑paragraph question was answered with four paragraphs less than an hour after my message; characteristic of Dick, he also pointed me to technical tools that could aid my query. He sent me a touching obituary he had written of his wife of more than sixty‑five years, Lois, who had just died and who had been his pillar in supporting him and raising their three children.

It is difficult not to view Garwin’s passing as something more than a personal loss. It is the departure of a type—perhaps the last of a type. A scientist who not only understood the arcana of physics, but who grasped the frailty of human institutions and the perils of unmediated power. A man who could, with equal ease, work out a thermonuclear cascade and dismantle a delusion in a Senate hearing room. That such a figure would exit the stage at a moment not just when the world sorely needs him but when the machinery of government not only disregards scientific counsel but actively spurns it – preferring instead the solipsistic comfort of invented facts fueled by ideological biases – renders his absence all the more acute. Garwin represented the moral and intellectual ballast that keeps a civilization grounded, and without which it begins to drift. There were a select few handful like him – Hans Bethe, Freeman Dyson, Sidney Drell. But he was the last. That we are now adrift makes his departure feel less like the close of a chapter than the dimming of the last light on the horizon. His life, to those who knew it, offers a retort to cynicism. In an age when expertise is increasingly sneered at, and when the distinction between persuasion and knowledge is recklessly blurred, Richard Garwin stood for the proposition that facts still matter, that thought must precede action, and that it is possible—however rarely—for brilliance to be in the service of restraint rather than abandon.

Brian Greene and John Preskill on Steven Weinberg

There's a very nice tribute to Steven Weinberg by Brian Greene and John Preskill that I came across recently that is worth watching. Weinberg was of course one of the greatest theoretical physicists of the later half of the 20th century, winning the Nobel Prize for one of the great unifications of modern physics, which was the unification of the electromagnetic and the weak forces. He was also a prolific author of rigorous, magisterial textbooks on quantum field theory, gravitation and other aspects of modern physics. And on top of it all, he was a true scholar and gifted communicator of complex ideas to the general public through popular books and essays; not just ideas in physics but ones in pretty much any field that caught his fancy. I had the great pleasure and good fortune to interact with him twice.

The conversation between Greene and Preskill is illuminating because it sheds light on many underappreciated qualities of Weinberg that enabled him to become a great physicist and writer, qualities that are worth emulating. Greene starts out by talking about when he first interacted with Weinberg when he gave a talk as a graduate student at the physics department of the University of Texas at Austin where Weinberg taught. He recalls how he packed the talk with equations and formal derivations, only to have the same concepts explained by Weinberg more clearly later. As physicists appreciate, while mathematics remains the key to unlock the secrets of the universe, being able to understand the physical picture is key. Weinberg was a master at doing both.

Preskill was a graduate student of Weinberg's at Harvard and he talks about many memories of Weinberg. One of the more endearing and instructive ones is from when he introduced Weinberg to his parents at his house. They were making ice cream for dinner, and Weinberg wondered aloud why we add salt while making the ice cream. By that time Weinberg had already won the Nobel Prize, so Preskill's father wondered if he genuinely didn't understand that you add the salt to lower the melting point of the ice cream so that it would stay colder longer. When Preskill's father mentioned this Weinberg went, "Of course, that makes sense!". Now both Preskill and Greene think that Weinberg might have been playing it up a bit to impress Preskill's family, but I wouldn't be surprised if he genuinely did not know; top tier scientists who work in the most rarefied heights of their fields are sometimes not as connected to basic facts as graduate students might be. 

More importantly, in my mind the anecdote illustrates an important quality that Weinberg had and that any true scientist should have, which is to never hesitate to ask even simple questions. If, as a Nobel Prize winning scientist, you think you are beyond asking simple questions, especially when you don't know the answers, you aren't being a very good scientist. The anecdote demonstrates a bigger quality that Weinberg had which Preskill and Greene discuss, which was his lifelong curiosity about things that he didn't know. He never hesitated to pump people for information about aspects of physics he wasn't familiar with, not to mention another disciplines. Freeman Dyson who I knew well had the same quality: both Weinberg and Dyson were excellent listeners. In fact, asking the right question, whether it was about salt and ice cream or about electroweak unification, seems to have been a signature Weinberg quality that students should take to heart.

Weinberg became famous for a seminal 1967 paper that unified the electromagnetic and weak force (and used ideas developed by Peter Higgs to postulate what we now call the Higgs boson). The title of the paper was "A Model of Leptons", but interestingly, Weinberg wasn't much of a model builder. As Preskill says, he was much more interested in developing general, overarching theories than building models, partly because models have a limited applicability to a specific domain while theories are much more general. This is a good point, but of course, in fields like my own field of computational chemistry, the problem isn't that there are no general theoretical frameworks  - there are, most notably the frameworks of quantum mechanics and statistical mechanics - but that applying them to practical problems is too complicated unless we build specific models. Nevertheless, Weinberg's attitude of shunning specific models for generality is emblematic of the greatest scientists, including Newton, Pauling, Darwin and Einstein.

Weinberg was also a rather solitary researcher; as Preskill points out, of his 50 most highly cited papers, 42 are written alone. He admitted himself in a talk that he wasn't the best collaborator. This did not make him the best graduate advisor either, since while he was supportive, his main contribution was more along the lines of inspiration rather than guidance and day-to-day conversations. He would often point students to papers and ask them to study them themselves, which works fine if you are Brian Greene or John Preskill but perhaps not so much if are someone else. In this sense Weinberg seems to be have been a bit like Richard Feynman who was a great physicist but who also wasn't the best graduate advisor.

Finally, both Preskill and Greene touch upon Weinberg's gifts as a science writer and communicator. More than many other scientists, he never talked down to his readers because he understood that many of them were as smart as him even if they weren't physicists. Read any one of his books and you see him explaining even simple ideas, but never in a way that assumes his audience are dunces. This is a lesson that every scientist and science writer should take to heart.

Greene especially knew Weinberg well because he invited him often to the World Science Festival which he and his wife had organized in New York over the years. The tribute includes snippets from Weinberg talking about the current and future state of particle physics. In the last part, an interviewer asks him about what is arguably the most famous sentence from his popular writings. In the last part of his first book, "The First Three Minutes", he says, "The more the universe seems comprehensible, the more it seems pointless." Weinberg's eloquent response when he was asked what this means sums up his life's philosophy and tells us why he was so unique, as a scientist and as a human being:

"Oh, I think everything's pointless, in the sense that there's no point out there to be discovered by the methods of science. That's not to say that we don't create points for our lives. For many people it's their loved ones; living a life of helping people you love, that's all the point that's needed for many people. That's probably the main point for me. And for some of us there's a point in scientific discovery. But these points are all invented by humans and there's nothing out there that supports them. And it's better that we not look for it. In a way, we are freer, in a way it's more noble and admirable to give points to our lives ourselves rather than to accept them from some external force."

Complementarity And The World: Niels Bohr’s Message In A Bottle

Werner Heisenberg was on a boat with Niels Bohr and a few friends, shortly after he discovered his famous uncertainty principle in 1927. A bedrock of quantum theory, the principle states that one cannot determine both the velocity and the position of particles like electrons with arbitrary accuracy. Heisenberg’s discovery foretold of an intrinsic opposition between these quantities; better knowledge of one necessarily meant worse knowledge of the other. Talk turned to physics, and after Bohr had described Heisenberg’s seminal insight, one of his friends quipped, “But Niels, this is not really new, you said exactly the same thing ten years ago.”

In fact, Bohr had already convinced Heisenberg that his uncertainty principle was a special case of a more general idea that Bohr had been expounding for some time – a thread of Ariadne that would guide travelers lost through the quantum world; a principle of great and general import named the principle of complementarity.

Complementarity arose naturally for Bohr after the strange discoveries of subatomic particles revealed a world that was fundamentally probabilistic. The positions of subatomic particles could not be assigned with definite certainty but only with statistical odds. This was a complete break with Newtonian classical physics where particles had a definite trajectory, a place in the world order that could be predicted with complete certainty if one had the right measurements and mathematics at hand. In 1925, working at Bohr’s theoretical physics institute in Copenhagen, Heisenberg was Bohr’s most important protégé had invented quantum theory when he was only twenty-four. Two years later came uncertainty; Heisenberg grasped that foundational truth about the physical world when Bohr was away on a skiing trip in Norway and Heisenberg was taking a walk at night in the park behind the institute.

When Bohr came back he was unhappy with the paper Heisenberg had written, partly because he thought the younger man seemed to echo his own ideas, but more understandably because Bohr – a man who was exasperatingly famous for going through a dozen drafts of a scientific paper and several drafts of even private letters – thought Heisenberg had not expressed himself clearly enough. The 42-year-old kept working on the 26-year-old until the latter admitted that “the uncertainty relations were just a special case of the more general complementarity principle.”

So what was this complementarity principle? Simply put, it was the observation that there are many truths about the world and many ways of seeing it. These truths might appear divergent or contradictory, but they are all equally essential in representing the true nature of reality; they are complementary. As Bohr famously put it, “The opposite of a big truth is also a big truth”. Complementarity provided a way to reconcile the paradoxes that seemed to bedevil quantum theory’s interpretation of reality.

The central scientific paradox was what is called wave-particle duality. In 1803, the British polymath Thomas Young had proposed that light, contrary to Isaac Newton’s view of it, consists of waves; an experiment like diffraction makes this wave nature clear. A hundred years later, in 1905, Einstein proposed that light in fact consists of particles, an idea he invoked in order to explain the photoelectric effect and which won him a Nobel Prize; these particles were later called photons. Soon it was found through other experiments that all subatomic particles and not just photons could display wave and particle behavior. In 1924, the French physicist and aristocrat Louis de Broglie saw a way through the impasse when he came up with a simple equation that related the momentum of a particle – a particle property – inversely to its wavelength – a wave property.

In spite of de Broglie’s insight, particles clearly don’t look like waves and waves don’t look like particles in real life. In fact the very names seem to put them at odds with one another. It was Bohr who saw both the problem and the solution. Particles and waves both exist and are equally valid and essential ways of interpreting the quantum world. Depending on what experiment you do you might see one or the other and never both, but they are not contradictory, they are complementary. Most crucially, you simply cannot make sense of reality without having both in hand. It was a powerful insight that cut through the complexities of intuition and language; it was not too different in principle from other counterintuitive truths that science has uncovered, for instance the truth that both lighter and heavier bodies fall at the same rate. Complementarity rationalized opposing tendencies of the physical world and indicated that they were one. It was what had made Bohr subsume the opposing quantities in Heisenberg’s uncertainty principle under the same rubric.

Complementarity was also pregnant with far more general interpretation. The most effective application of it to human affairs in Bohr’s hands was the problem posed by nuclear weapons. Even before the bomb had been used on Hiroshima, Bohr saw deeper and further than anyone else that the very fact that nuclear weapons are so enormously destructive might make them the most potent force for peace that the world has ever seen, simply because statesmen will realize that nobody can truly “win” a nuclear war if everyone has them. “We are in a completely new situation that cannot be resolved by war”, Bohr said. The complementarity of the bomb continues to keep the peace through deterrence.

Another noteworthy example was a speech delivered by Bohr in 1938 to the International Congress of Anthropological and Ethnological Sciences at Kronberg Castle in Denmark. Apologizing at the outset for presuming to speak about a topic on which he was not an expert, Bohr proceeded to provide a succinct summary of complementarity in the context of atomic physics. Turning to biology, he then made the perspicacious observation – still the subject of considerable debate – that reason and instinct which might appear to be opposed to each other are complementary, both providing a complete picture of a sentient being. Bohr then came to the crux of the matter, pointing out that complementarity is of the essence when people are judging other cultures which might seem divergent from their own but which turn out to be different and equally productive ways of looking at the world. As Bohr eloquently put it: “Each culture represents a harmonious balance of traditional conventions by means of which latent potentialities of human life can unfold themselves in a way which reveals to us new aspects of its unlimited richness and variety.” Bohr believed that contact between cultures can go a long way in not just dispelling biases but in mutually enriching both parties: “A more or less intimate contact between different human societies can lead to a gradual fusion of traditions, giving birth to a quite new culture”. This is as clear an appeal for internationalism and mutual understanding that one can think of; if everyone had understood complementarity, maybe we might have had less fascism, imperialism and genocide. The final goal of complementary views of societies, as Bohr pointed out powerfully in the same lecture, isn’t different from the goal of science as a whole – it is “the gradual removal of prejudices”.

As we approach what seem to be novel problems in the 21st century, Bohr’s complementarity is a message in a bottle from one fraught world to another, telling us that seeing these new problems through the lens of an old principle can be most rewarding. We seem to live in a time when many see social and political problems through a binary, black-or-white, zero sum lens. Either my viewpoint is right or yours, but not both. Complementarity bridges that division. For instance consider the problem of individualism vs communalism, a divide that also hints at the cultural divide Bohr spoke about, in this case largely an Eastern vs Western divide. Western society is fiercely individualistic; self-interests guide people’s lives and most people don’t want others to tell them that they should live their lives for others. Meanwhile, Eastern and some European societies are much more communal; community interests often override self-interest and individuals are told that their self-development should take a backseat to the development of their community and society. Bohr’s complementarity tells us that this divergent view should not exist. Communal and individualistic views are both essential for looking at the world and building a more productive society; in fact one can gain self-knowledge and wisdom by working for a community, and likewise a community can be improved when people engage in individualistic self-improvement that helps everyone.

There are other problems for which complementarity provides a potential solution. I will speak mostly for the United States since that’s where I live, but these problems are in fact global. Consider the problem of immigration, one to which Bohr’s 1938 address is directly applicable. People criticized as “globalists” think that unfettered immigration is a net good. The opposing camp thinks that preserving a nation’s culture is important, and too much or too rapid immigration will weaken this culture. But complementarity tells us that nationalism is in fact strengthened when immigrants work together for the common good of the country. At the same time, immigrants should put their country first and prioritize work that will strengthen their nation’s economy, military and social institutions. We are global citizens, but we are also shaped by evolution and culture to take care of our immediate own. The opposite of a big truth is also a big truth.

Even scientific debates like the nature (genes) vs nurture (environment) conundrum can benefit from complementary views. People criticized as biological “essentialists” believe that genes dictate a lot of an individual’s physical and psychological makeup while the opposing “nurture” camp believes that much of the effect of genes can be changed by the environment. But complementarity says that just like the joint wave-particle view of reality, individuals are whole and complete, and this wholeness arises from a combination of genes and environment. In that sense, how much of a person’s mental and physical constitution we can control by either manipulating their genes or their environment is almost irrelevant. What’s relevant is the basic understanding in the first place that both matter; even if both camps agree with this baseline, they would already be talking a lot more with each other.

A third application of complementarity to international affairs, one which stems directly from Bohr’s view of the complementarity of the bomb, is to the relationship between United States and China, a relationship which will likely be the single-most important geopolitical determinant of the 21st century. China clearly has an autocratic regime that is not likely to yield to demands for more democratic behavior, both internally and externally, anytime soon. This has led to many in the United States to regard China as an implacable foe, almost a second Soviet Union. An important consequence of this view has been to see almost every technological development in the two countries, from gene editing to artificial intelligence to new weapons, as a contest.

But irrespective of the moral wisdom of engaging in this contest, complementarity tells us that such contests are likely to lead to the mutual ruin of both China and the United States, and by extension the rest of the world; for the same reason that any arms race would hollow out countries’ coffers and ramp up the specter of mutual annihilation. The reason is simple: both computer code and the physics of nuclear weapons are products of the fundamental laws of science and technology discovered or invented by human minds. Both can be divined and implemented by any country with smart scientists and engineers, which basically means any developing or developed country. An arms race in AI between China and the United States, for instance, would be as futile and dangerous as was the nuclear arms race between the United States and the former Soviet Union. Both countries would be fooling themselves if they think they can write better computer code and keep it secret for a long time. In that sense the fact that computer code, just like nuclear fission, is essentially a discovery of the human mind poses inconvenient truths for both countries. Whether we like it or not, we need to realize the complementarity of artificial intelligence akin to how we grudgingly realized the complementarity of the bomb: we need to realize that AI is powerful, that it is dangerous, that its secrets cannot stay secret for very long, that there are no real defenses against it, that the very dangers of AI cry for peaceful solutions to AI, and therefore that mutual cooperation between China and the United States under an umbrella of an international organization like the United Nations would be the only solution to avoid mutual cyber-destruction. China might be autocratic, but it has self-interests and wouldn’t want to see its own ruin. In the end, harmony between the United States and China might not be forced by bridging the moral divide between the two countries’ social and political systems: it would be forced by the very laws of science and technology.

Without oversimplifying the issue, it’s clear to me that Bohr’s complementarity provides a mediating middle ground for almost any other social or political issue I can think of; it’s not so much that it offers a solution but that it will compel each side to see the importance of the other side’s argument in providing a complete view of reality that cannot be provided by either viewpoint by itself. Pro-life or pro-choice? One can respect both the life of an unborn child and the life of the mother; the two are complementary. Socialism or capitalism? One can certainly have a mixed market economy – of the kind found in Niels Bohr’s home country for instance – that would give us the benefits of both. Climate legislation or rapid economic growth? One can create jobs related to new climate technologies that will result in economic growth. Science or religion? They address complementary aspects of the world, Stephen Jay Gould’s “non-overlapping magisteria”.

If we accept the idea of complementarity, we are in essence accepting the validity of all ways of looking at the world, and not just one. This does not mean that all ways are equally right – we can’t accept the germ theory of disease and the “theory” of diseases as a punishment from God on equal terms – but it is precisely through placing them on a level playing field and letting them play out their logical flow that we can even know how much of which view is right. In addition, Bohr realized that the world is indeed gray, that even flawed visions may contain snatches of truth that should be acknowledged as potential building blocks in our view of reality. But ultimately, Bohr’s plea for complementarity was a plea for what he called an “open world”, an ideal that for him was the highest that the peoples of the world could aspire to, an ideal that arose naturally from the democratic republic of science. If we accept complementarity, we automatically become open to examining every single approach to a problem, every way of parsing reality. Most importantly, we become open to true, unfettered communication with our fellow human beings, a tentative but lasting step toward Bohr’s – and science’s – “gradual removal of prejudices”. That seems like an important message for today.

First published on 3 Quarks Daily.

Steven Weinberg (1933-2021)

I was quite saddened to hear about the passing of Steven Weinberg, perhaps the dominant living figure from the golden age of particle physics. I was especially saddened since he seemed to be doing fine, as indicated by a lecture he gave at the Texas Science Festival this March. I think many of us thought that he was going to be around for at least a few more years. 

Weinberg was one of a select few individuals who transformed our understanding of elementary particles and cemented the creation of the Standard Model (he coined the name), in his case by unifying the electromagnetic and weak forces; for this he shared the 1979 Nobel Prize in physics with Abdus Salam and Sheldon Lee Glashow. His 1967 paper which heralded the unification, "A Model of Leptons", was only 3 pages long and remains one of the most highly cited articles in physics history.

But what made Weinberg special was that he was not only one of the most brilliant theoretical physicists of the 20th century but also a pedagogical master with few peers. His many technical textbooks, especially his 3-volume "Quantum Theory of Fields", have educated a generation of physicists; meanwhile, his essays in the New York Times Book Review and other avenues and collections of articles published as popular books have educated the lay public about the mysteries of physics. But in his popular books Weinberg also revealed himself to be a real Renaissance Man, writing not just about physics but about religion, politics, philosophy, history including the history of science, opera and literature. He was also known for his political advocacy of science. Among scientists of his generation, only Freeman Dyson had that kind of range.

There have been some great tributes to him, and I would point especially to the ones by Scott Aaronson and Robert McNees, both of whom interacted with Weinberg as colleagues. The tribute by Scott especially shows the kind of independent streak that Weinberg had, never content to go with the mainstream and always seeking orthogonal viewpoints and original thoughts. In that he very much reminded me of Dyson; the two were in fact friends and served together on the government advisory group JASON, and my conversation with Weinberg which I describe below ended with him asking me to give my regards to Freeman, who I was meeting in a few weeks.

I had the good fortune of interacting with Steve on two occasions, both rewarding. The first time I had the opportunity to be with him on a Canadian television panel on the challenges of Big Science. You can see the discussion here:

https://www.tvo.org/video/the-challenge-of-big-science

The next time was a few years later when I contacted him about a project and asked whether he had some thoughts to share about it. Steve didn't know me personally (although he did remember the Big Science panel) and was even then very busy with writing and other projects. In addition, the project wasn't something close to his immediate interests, so I was surprised when not only did he respond right away but asked me to call him at 10 AM on a Sunday and spoke generously for more than an hour. I still have the recording.

Steve was a great physicist, a gentleman and a Renaissance Man, a true original. We are unlikely to see the likes of him for a long time. 

One of the reasons I feel particularly wistful with his passing is because he was among the last of the creators of modern particle physics. He worked in an enormously fruitful time in which theory went hand in hand with experiment. This is different from the last twenty years in which fundamental physics and especially string theory have been struggling to make experimental connections. In cosmology however, there have been very exciting developments, and Weinberg who devoted his last few decades to the topic was certainly very interested in these. Hopefully fundamental physics can become as involved with the productive interplay of theory and experiment as cosmology and condensed matter physics are, and hopefully we can again resurrect the golden era of science in which Steven Weinberg played such a commanding role.

Brains, Computation And Thermodynamics: A View From The Future?

Progress in science often happens when two or more fields productively meet. Astrophysics got a huge boost when the tools of radio and radar met the age-old science of astronomy. From this fruitful marriage came things like the discovery of the radiation from the big bang. Another example was the union of biology with chemistry and quantum mechanics that gave rise to molecular biology. There is little doubt that some of the most important future discoveries in science in the future will similarly arise from the accidental fusion of multiple disciplines.

One such fusion sits on the horizon, largely underappreciated and unseen by the public. It is the fusion between physics, computer science and biology. More specifically, this fusion will likely see its greatest manifestation in the interplay between information theory, thermodynamics and neuroscience. My prediction is that this fusion will be every bit as important as any potential fusion of general relativity with quantum theory, and at least as important as the development of molecular biology in the mid 20th century. I also believe that this development will likely happen during my own lifetime.

The roots of this predicted marriage go back to 1867. In that year the great Scottish physicist James Clerk Maxwell proposed a thought experiment that was later called ‘Maxwell’s Demon’. Maxwell’s Demon was purportedly a way to defy the second law of thermodynamics that had been proposed a few years earlier. The second law of thermodynamics is one of the fundamental laws governing everything in the universe, from the birth of stars to the birth of babies. It basically states that left to itself, an isolated system will tend to go from a state of order to one of disorder. A good example is how a bottle of perfume wafts throughout a room with time. This order and disorder was quantified by a quantity called entropy.

In technical terms, the order and disorder refers to the number of states a system can exist in; order means fewer states and disorder means more. The second law states that isolated systems will always go from fewer states and lower entropy (order) to more states and higher entropy (disorder). Ludwig Boltzmann quantified this relationship with a simple equation carved on his tombstone in Vienna: S = klnW, where k is a constant called the Boltzmann constant, ln is the natural logarithm (to the base e) and W is the number of states.

Maxwell’s Demon was a mischievous creature which sat on top of a box with a partition in the middle. The box contains molecules of a gas which are ricocheting in every direction. Maxwell himself had found that these molecules’ velocities follow a particular distribution of fast and slow. The demon observes these velocities, and whenever there is a molecule moving faster than usual in the right side of the box, he opens the partition and lets it into the left side, quickly closing the partition. Similarly he lets in slower moving molecules from left to right. After some time, all the slow molecules will be in the right side and the fast ones will in the left. Now, velocity is related to temperature, so this means that one side of the box has heated up and the other has cooled down. To put it another way, the box went from a state of random disorder to order. According to the second law this means that the entropy of the system of the system decreased, which is impossible.

Maxwell’s demon seemingly contravenes the second law of thermodynamics (University of Pittsburgh)

For the next few years scientists tried to get around Maxwell’s Demon’s paradox, but it was in 1922 that the Hungarian physicist Leo Szilard made a dent in it when he was a graduate student hobnobbing with Einstein, Planck and other physicists in Berlin. Szilard realized an obvious truth that many others seem to have missed. The work and decision-making that the demon does to determine the velocities of the molecules itself generates entropy. If one takes this work into account, it turns out that the total entropy of the system has indeed increased. The second law is safe. Szilard later went on to a distinguished career as a nuclear physicist, patenting a refrigerator with Einstein and becoming the first person to think of a chain reaction.

Perhaps unknowingly, however, Szilard had also discovered a connection – a fusion of two fields – that was going to revolutionize both science and technology. When the demon does work to determine the velocities of molecules, the entropy that he creates comes not just from the raising and lowering of the partition but from his thinking processes, and these processes involve information processing. Szilard had discovered a crucial and tantalizing link between entropy and information. Two decades later, mathematician Claude Shannon was working at Bell Labs, trying to improve the communication of signals through wires. This was unsurprisingly an important problem for a telephone and communications company. The problem was that when engineers were trying to send a message over a wire, it would lose its quality because of many factors including noise. One of Shannon’s jobs was to figure out how to make this transmission more efficient.

Shannon found out that there is a quantity that relates to the information transmitted over the wire. In crude terms, this quantity was inversely related to the information as well as to the probability of transmitting that information; the higher the probability of transmitting accurate information over a channel, the lower this quantity was and vice versa. When Shannon showed his result to the famous mathematician John von Neumann, von Neumann with his well-known lightning-fast ability to connect disparate ideas, immediately saw what it was: “You should call your function ‘entropy’”, he said, “firstly because that is what it looks like in thermodynamics, and secondly because nobody really knows what entropy is, so in a debate you will always have the upper hand.” Thus was born the connection between information and entropy. Another fortuitous connection was born – between information, entropy and error or uncertainty. The greater the uncertainty in transmitting a message, the greater the entropy, so entropy also provided a way to quantify error. Shannon’s 1948 paper, “A Mathematical Theory of Communication”, was a seminal publication and has been called the Magna Carta of the information age.

Even before Shannon, another pioneer had published a paper that laid the foundations of the theory of computing. In 1936 Alan Turing published “On Computable Numbers, with an Application to the Entscheidungsproblem”. This paper introduced the concept of Turing machines which also process information. But neither Turing nor von Neumann really made the connection between computation, entropy and information explicit. Making it explicit would take another few decades. But during those decades, another fascinating connection between thermodynamics and information would be discovered.

Stephen Hawking’s tombstone at Westminster Abbey (Cambridge News)

That connection came from Stephen Hawking getting annoyed. Hawking was one of the pioneers of black holes, and along with Roger Penrose he had discovered that at the center of every black hole is a singularity that warps spacetime infinitely. The boundary of the black hole is its event horizon and within that boundary not even light can escape. But black holes posed some fundamental problems for thermodynamics. Every object contains entropy, so when an object disappears into a black hole, where does its entropy go? If the entropy of the black hole does not increase then the second law of thermodynamics would be violated. Hawking had proven that the area of a black hole’s event horizon never decreases, but he had pushed the thermodynamic question under the rug. In 1972 at a physics summer school, Hawking met a graduate student from Princeton named Jacob Bekenstein who proposed that the increasing area of the black hole was basically a proxy for its increasing entropy. This annoyed Hawking and he did not believe it because increased entropy is related to heat (heat is the highest- entropy form of energy) and black holes, being black, could not radiate heat. With two colleagues Hawking set out to prove Bekenstein wrong. In the process, he not only proved him right but also made what is considered his greatest breakthrough: he gave black holes a temperature. Hawking found out that black holes do emit thermal radiation. This radiation can be explained when you take quantum mechanics into account. The Hawking-Bekenstein discovery was a spectacular example of another fusion: between information, thermodynamics, quantum mechanics and general relativity. Hawking deemed it so important that he wanted to put it on his tombstone in Westminster Abbey, and so it has been.

This short digression was to show that more links between information, thermodynamics and other disciplines were being forged in the 1960s and 70s. But nobody saw the connections between computation and thermodynamics until Rolf Landauer and Charles Bennett came along. Bennett and Landauer were both working at IBM. Landauer was an émigré who fled from Nazi Germany before working for the US Navy as an electrician’s mate, getting his PhD at Harvard and joining IBM. IBM was then a pioneer of computing; among other things they had built computers for the Manhattan Project. In 1961, Landauer published a paper titled “Irreversibility and Heat Generation in the Computing Process” that is destined to become a classic of science. In it, Landauer established that the basic act of computation – the change of one bit to another, say a 1 to a 0 – requires a bare minimum amount of entropy. He quantified this amount with another simple equation: S = kln2, with k again being the Boltzmann constant and ln the natural logarithm. This has become known as the Landauer bound; it is the absolute minimum amount of entropy that has to be expended in a single bit operation. Landauer died in 1999 and as far as I know the equation is not carved on his tombstone.

The Landauer bound applies to all kinds of computation in principle and biological processes are also a form of information processing and computation, so it’s tantalizing to ask whether Landauer’s calculation applies to them. Enter Charles Bennett. Bennett is one of the most famous scientists whose name you may not have heard of. He is not only one of the fathers of quantum computing and quantum cryptography but he is also one of the two fathers of the marriage of thermodynamics with computation, Landauer being the other. Working with Landauer in the 1970s and 80s, Bennett applied thermodynamics to both Turing machines and biology. By good fortune he had gotten his PhD in physical chemistry studying the motion of molecules, so his background primed him to apply ideas from computation to biology.

Charles Bennett from IBM has revolutionized our understanding of the thermodynamics of computation (AMSS)

To simplify matters, Bennett considered what he called a Brownian Turing machine. Brownian motion is the random motion of atoms and molecules. A Brownian Turing machine can write and erase characters on a tape using energy extracted from a random environment. This makes the Brownian Turing machine reversible. A reversible process might seem strange, but in fact it’s found in biology all the time. Enzyme reactions occur from the reversible motion of chemicals – at equilibrium there is equal probability that an enzymatic reaction will go forward or backward. What makes these processes irreversible is the addition of starting materials or the elimination of chemical products. Even in computation, only a process which erases bits is truly irreversible because you lose information. Bennett envisaged a biological process like protein translation as a Brownian Turing machine which adds or subtracts a molecule like an amino acid, and he calculated the energy and entropy expenditures involved in running this machine. Visualizing translation as a Turing machine made it easier to do a head-to-head comparison between biological processes and bit operations. Bennett found out that if the process is reversible the Landauer bound does not hold and there is no minimum entropy required. Real life of course is irreversible, so how do real-life processes compare to the Landauer bound?

In 2017, a group of researchers published a fascinating paper in the Philosophical Transactions of the Royal Society in which they explicitly calculated the thermodynamic efficiency of biological processes. Remarkably, they found that the efficiency of protein translation is several orders of magnitude better than the best supercomputers, in some cases as better as a million fold. More remarkably, they found that the efficiency is only one order of magnitude worse than the theoretical minimum Landauer bound. In other words, evolution has done one hell of a job in optimizing the thermodynamic efficiency of biological processes.

But not all biological processes. Circling back to the thinking processes of Maxwell’s little demon, how does this efficiency compare to the efficiency of the human brain? Surprisingly, it turns out that neural processes like the firing of synapses are estimated to be much worse than protein translation and more comparable to the efficiency of supercomputers. At first glance, the human brain thus appears to be worse than other biological processes. However, this seemingly low computational efficiency of the brain must be compared to its complex structure and function. The brain weighs only about a fiftieth of the weight of an average human but it uses up 20% of the body’s energy. It might seem that we are simply not getting the biggest bang for our buck, with an energy-hungry brain providing low computational efficiency. What would explain this inefficiency and this paradox?

My guess is that the brain has been designed to be inefficient through a combination of evolutionary accident and design and that efficiency is the wrong metric for gauging the performance of the brain. Efficiency is the wrong metric because thinking of the brain in digital terms is the wrong metric. The brain arose through a series of modular inventions responding to new environments created by both biology and culture. We now know that thriving in these environments needed a combination of analog and digital functions.; for instance, the nerve impulses controlling blood pressure are digital while the actual change in pressure is continuous and analog. It is likely that digital neuronal firing is built on an analog substrate of wet matter, and that higher-order analog functions could be emergent forms of digital neuronal firing. As early as the 1950s, von Neumann conjectured that we would need to model the brain as both analog and digital in order to understand it. Around the time that Bennett was working out the thermodynamics of computation, two mathematicians named Marian Pour-El and Ian Richards proved a very interesting theorem which showed that in certain cases, there are numbers that are not computable with digital computers but are computable with analog processes; analog computers are thus more powerful in such cases.

If our brains are a combination of digital and analog, it’s very likely that they are this way so that they can span a much bigger range of computation. But this bigger range would come at the expense of inefficiency in the analog computation process. The small price of lower computational efficiency as measured by the Landauer bound would come at the expense of the much greater evolutionary benefits of performing complex calculations that allow us to farm, build cities, know stranger from kin and develop technology. Essentially, the Landauer bound could be evidence for the analog nature of our brains. There is another interesting fact about analog computation, which is its greater error rate; digital computers took off precisely because they had low error rates. How does the brain function so well in spite of this relatively high error rate? Is the brain consolidating this error when we dream? And can we reduce this error rate by improving the brain’s efficiency? Would that make our brains better or worse at grasping the world?

From the origins of thermodynamics and Maxwell’s Demon to the fusion of thermodynamics with information processing, black holes, computation and biology, we have come a long way. The fusion of thermodynamics and computation with neuroscience just seems to be beginning, so for a young person starting out in the field the possibilities are exciting and limitless. A multitude of general questions abound: How does the efficiency of the brain relate to its computational abilities? What might be the evolutionary origins of such abilities? What analogies between the processing of information in our memories and that in computers might we discover through this analysis? And finally, just like Shannon did for information, Hawking and Bekenstein did for black holes and Landauer and Bennett did for computation and biology, can we find out a simple equation describing how the entropy of thought processes relates to simple neural parameters connected to memory, thinking, empathy and emotion? I do not know the answers to these questions, but I am hoping someone who is reading this will, and at the very least they will then be able to immortalize themselves by putting another simple formula describing the secrets of the universe on their tombstone.

Further reading:

1. Charles Bennett – The Thermodynamics of Computation
2. Seth Lloyd – Ultimate Physical Limits to Computation
3. Freeman Dyson – Are brains analog or digital?
4. George Dyson – Analogia: The Emergence of Technology Beyond Programmable Control (August 2020)
5. Richard Feynman – The Feynman Lectures on Computation (Chapter 5)
6. John von Neumann – The General and Logical Theory of Automata

First published on 3 Quarks Daily

The Fermi-Pasta-Ulam-Tsingou Problem: A Foray Into The Beautifully Simple And The Simply Beautiful

In November 1918, a 17-year-student from Rome sat for the entrance examination of the Scuola Normale Superiore in Pisa, Italy’s most prestigious science institution. Students applying to the institute had to write an essay on a topic that the examiners picked. The topics were usually quite general, so the students had considerable leeway. Most students wrote about well-known subjects that they had already learnt about in high school. But this student was different. The title of the topic he had been given was “Characteristics of Sound”, and instead of stating basic facts about sound, he “set forth the partial differential equation of a vibrating rod and solved it using Fourier analysis, finding the eigenvalues and eigenfrequencies. The entire essay continued on this level which would have been creditable for a doctoral examination.” The man writing these words was the 17-year-old’s future student, friend and Nobel laureate, Emilio Segre. The student was Enrico Fermi. The examiner was so startled by the originality and sophistication of Fermi’s analysis that he broke precedent and invited the boy to meet him in his office, partly to make sure that the essay had not been plagiarized. After convincing himself that Enrico had done the work himself, the examiner congratulated him and predicted that he would become an important scientist.

Twenty five years later Fermi was indeed an important scientist, so important in fact that J. Robert Oppenheimer had created an entire division called F-Division under his name at Los Alamos, New Mexico to harness his unique talents for the Manhattan Project. By that time the Italian emigre was the world’s foremost nuclear physicist as well as perhaps the only universalist in physics – in the words of a recent admiring biographer, “the last man who knew everything”. He had led the creation of the world’s first nuclear reactor in a squash court at the University of Chicago in 1942 and had won a Nobel Prize in 1938 for his work on using neutrons to breed new elements, laying the foundations of the atomic age.

The purpose of F-division was to use Fermi’s unprecedented joint abilities in both experimental and theoretical physics to solve problems that stumped others. To Fermi other scientists would take their problems in all branches of physics, many of them current or future Nobel laureates. They would take advantage of Fermi’s startlingly simple approach to problem-solving, where he would first qualitatively estimate the parameters and solution and then plug in complicated mathematics only when necessary to drive relentlessly toward the solution. He had many nicknames including “The Roadroller”, but the one that stuck was “The Pope” because his judgement on any physics problem was often infallible and the last word.

Fermi’s love for semi-quantitative, order-of-magnitude estimates gave him an unusual oeuvre. He loved working out the most rigorous physics theories as much as doing back-of-the-envelope calculations designed to test ideas; the latter approach led to the famous set of problems called ‘Fermi problems‘. Simplicity and semi-quantitative approaches to problems are the hallmark of models, and Fermi inevitably became one of the first modelers. Simple models such as the quintessential “spherical cow in a vacuum” are the lifeblood of physics, and some of the most interesting insights have come from using such simplicity to build toward complexity. Interestingly, the problem that the 17-year-old Enrico had solved in 1918 would inspire him in a completely novel way many years later. It would be the perfect example of finding complexity in simplicity and would herald the beginnings of at least two new, groundbreaking fields.

Los Alamos was an unprecedented exercise in bringing a century’s worth of physics, chemistry and engineering to bear on problems of fearsome complexity. Scientists quickly realized that the standard tools of pen and paper that they had been using for centuries would be insufficient, and so for help they turned to some of the first computers in history. At that time the word “computer” meant two different things. One meaning was women who calculated. The other meaning was machines which calculated. Women who were then excluded from most of the highest echelons of science were employed in large numbers to perform repetitive calculations on complicated physics problems. Many of these problems at Los Alamos were related to the tortuous flow of neutrons and shock waves from an exploding nuclear weapon. Helping the female computers were some of the earliest punched card calculators manufactured by IBM. Although they didn’t know it yet, these dedicated women working on those primitive calculators became history’s first pioneering programmers. They were the forerunners of the women who worked at NASA two decades later on the space program.

Fermi had always been interested in these computers as a way to speed up calculations or to find new ways to do them. At Los Alamos a few other far-seeing physicists and mathematicians had realized their utility, among them the youthful Richard Feynman who was put in charge of a computing division. But perhaps the biggest computing pioneer at the secret lab was Fermi’s friend, the dazzling Johnny von Neumann, widely regarded as the world’s foremost mathematician and polymath and fastest thinker. Von Neumann who had been recruited by Oppenheimer as a consultant because of his deep knowledge of shock waves and hydrodynamics had become interested in computers after learning that a new calculating machine called ENIAC was being built at the University of Pennsylvania by engineers J. Presper Eckert, John Mauchly, Herman Goldstine and others. Von Neumann realized the great potential of what we today call the shared program concept, a system of programming that contains both the instructions for doing something and the process itself in the same location, both coded in the same syntax.

Fermi was a good friend of von Neumann’s, but his best friend was Stanislaw Ulam, a mathematician of stunning versatility and simplicity who had been part of the famous Lwów School of mathematics in Poland. Ulam belonged to the romantic generation of Central European mathematics, a time during the early twentieth century when mathematicians had marathon sessions fueled by coffee in Lwów, Vienna and Warsaw’s famous cafes, where they scribbled on the marble tables and argued mathematics and philosophy late into the night. Ulam had come to the United States in the 1930s; by then von Neumann had already been firmly ensconced at Princeton’s Institute for Advanced Study with a select group of mathematicians and physicists including Einstein. Ulam had started his career in the most rarefied parts of mathematics including set theory; he later joked that during the war he had to stoop to the level of manipulating actual numbers instead of merely abstract symbols. After the war started Ulam had wanted to help with the war effort. One day he got a call from Johnny, asking him to a move to a secret location in New Mexico. At Los Alamos Ulam worked closely with von Neumann and Fermi and met the volatile Hungarian physicist Edward Teller with whom he began a fractious, consequential working relationship.

Fermi, Ulam and von Neumann all worked on the intricate calculations involving neutron and thermal diffusion in nuclear weapons and they witnessed the first successful test of an atomic weapon on July 16th, 1945. All three of them realized the importance of computers, although only von Neumann’s mind was creative and far-reaching enough to imagine arcane and highly significant applications of these as yet primitive machines – weather control and prediction, hydrogen bombs and self-replicating automata, entities which would come to play a prominent role in both biology and science fiction. After the war ended, computers became even more important in the early 1950s. Von Neumann and his engineers spearheaded the construction of a pioneering computer in Princeton. After the computer achieved success in doing hydrogen bomb calculations at night and artificial life calculations during the day, it was shut down because the project was considered too applied by the pure mathematicians. But copies started springing up at other places, including one at Los Alamos. Partly in deference to the destructive weapons whose workings would be modeled on it, the thousand ton Los Alamos machine was jokingly christened MANIAC, for Mathematical Analyzer Numerical Integrator and Computer. It was based on the basic plan proposed by von Neumann which is still the most common plan used for computers worldwide – the von Neumann architecture.

After the war, Enrico Fermi had moved to the University of Chicago which he had turned into the foremost center of physics research in the country. Among his colleagues and students there were T. D. Lee, Edward Teller and Subrahmanyan Chandrasekhar. But the Cold War imposed on his duties, and the patriotic Fermi started making periodic visits to Los Alamos after President Truman announced in 1951 that he was asking the United States Atomic Energy Commission to resume work on the hydrogen bomb as a top priority. Ulam joined him there. By that time Edward Teller had been single-mindedly pushing for the construction of a hydrogen bomb for several years. Teller’s initial design was highly flawed and would have turned into a dud. Working with pencil and paper, Fermi, Ulam and von Neumann all confirmed the pessimistic outlook for Teller’s design, but in 1951, Ulam had a revolutionary insight into how a feasible thermonuclear weapon could be made. Teller honed this insight into a practical design which was tested in November 1952, and the thermonuclear age was born. Since then, the vast majority of thermonuclear weapons in the world’s nuclear arsenals have been based on some variant of the Teller-Ulam design.

By this time Fermi had acutely recognized the importance of computers, to such an extent in fact that in the preceding years he had taught himself how to code. Work on the thermonuclear brought Fermi and Ulam together, and in 1955 Fermi proposed a novel project to Ulam. To help with the project Fermi recruited a visiting physicist named John Pasta who had worked as a beat cop in New York City during the Depression. With the MANIAC ready and standing by, Fermi was especially interested in problems where highly repetitive calculations on complex systems could take advantage of the power of computing. Such calculations would be almost impossible in terms of time to perform by hand. As Ulam recalled later,

“Fermi held many discussions with me on the kind of future problems which could be studied through the use of such machines. We decided to try a selection of problems for heuristic work where in the absence of closed analytic solutions experimental work on a computing machine might perhaps contribute to the understanding of properties of solutions. This could be particularly fruitful for problems involving the asymptotic, long time or “in the large” behavior of non-linear physical systems…Fermi expressed often a belief that future fundamental theories in physics may involve non-linear operators and equations, and that it would be useful to attempt practice in the mathematics needed for the understanding of non-linear systems. The plan was then to start with the possibly simplest such physical model and to study the results of the calculation of its long-term behavior.”

Fermi and Ulam had caught the bull by its horns. Crudely speaking, linear systems are systems where the response is proportional to the input. Non-linear systems are ones where the response can vary disproportionately. Linear systems are the ones which many physicists study in textbooks and as students. Non-linear systems include almost everything encountered in the real world. In fact, the word “non-linear” is highly misleading, and Ulam nailed the incongruity best: “To say that a system is non-linear is to say that most animals are non-elephants.” Non-linear systems are the rule rather than the exception, and by 1955 physics wasn’t really well-equipped to handle this ubiquity. Fermi and Ulam astutely realized that the MANIAC was ideally placed to attempt a solution to non-linear problems. But what kind of problem would be complex enough to attempt by computer, yet simple enough to provide insights into the workings of a physical system? Enter Fermi’s youthful fascination with vibrating rods and strings.

The simple harmonic oscillator is an entity which physics students encounter in their first or second year of college. Its distinguishing characteristic is that the force applied to it is proportional to the displacement. But as students are taught, this is an approximation. Real oscillators – real pendulums, real vibrating rods and strings in the real world – are not simple. The force applied results in a complicated function of the displacement. Fermi and Ulam set up a system consisting of a string attached to one end. They considered four models; one where the force is proportional to the displacement, one where the force is proportional to the square of the displacement, one where it’s proportional to the cube, and one where the displacement varies in a discontinuous way with the force, going from broken to linear and back. In reality the string was modeled as a series of 64 points all connected through these different forces. The four graphs from the original paper are shown below, with force on the x-axis and displacement on the y-axis and the dotted line indicating the linear case.

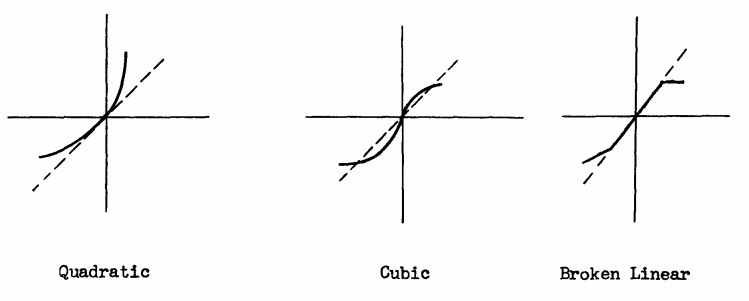
Here’s what the physicists expected: the case for a linear oscillator, familiar to physics students, is simple. The string shows a single sinusoidal node that remains constant. The expectation was that when the force became non-linear, higher frequencies corresponding to two, three and more sinusoidal modes would be excited (these are called harmonics or overtones). The global expectation was that adding a non-linear force to the system would lead to an equal distribution or “thermalization” of the energy, leading to all modes being excited and the higher modes being heavily so.

What was seen was something that was completely unexpected and startling, even to the “last man who knew everything.” When the quadratic force was applied, the system did indeed transition to the two and three-mode system, but the system then suddenly did something very different.

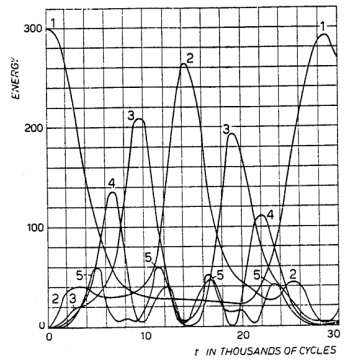
“Starting in one problem with a quadratic force and a pure sine wave as the initial position of the string, we indeed observe initially a gradual increase of energy in the higher modes as predicted. Mode 2 starts increasing first, followed by mode 3 and so on. Later on, however, this gradual sharing of energy among successive modes ceases. Instead, it is one or the other mode that predominates. For example, mode 2 decides, as it were, to increase rather rapidly at the cost of all other modes and becomes predominant. At one time, it has more energy than all the others put together! Then mode 3 undertakes this role.”

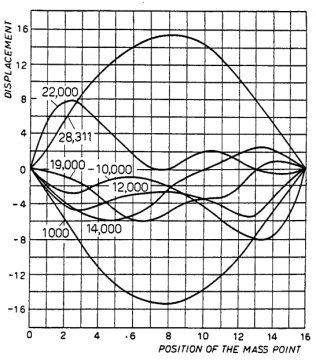
Fermi and Ulam could not resist adding an exclamation point even in the staid language of scientific publication. Part of the discovery was in fact accidental; the computer had been left running overnight, giving it enough time to go through many more cycles. The word “decides” is also interesting; it’s as if the system seems to have a life of its own and starts dancing of its own volition between one or two lower modes; Ulam thought that the system was playing a game of musical chairs. Finally it comes back to mode 1, as if it were linear, and then continues this periodic behavior. An important way to describe this behavior is to say that instead of the initial expectation of equal distribution of energy among the different modes, the system seems to periodically concentrate most or all of its energy in one or a very small number of modes. The following graph for the quadratic case makes this feature clear: on the y-axis is energy while on the x-axis is the number of cycles ranging into the thousands (as an aside, this very large number of cycles is partly why it would be impossible to solve this problem using pen and paper in reasonable time). As is readily seen, the height of modes 2 and 3 is much larger than the higher modes.

The actual shapes of the string corresponding to this asymmetric energy exchange are even more striking, indicating how the lower modes are disproportionately excited. The large numbers here again correspond to the number of cycles.

The graphs for the cubic and broken displacement case are similar but even more complex, leading to higher modes being excited more often but the energy still concentrated into the lower modes. Needless to say, these results were profoundly unexpected and fascinating. The physicists did not quite know what to make of them, and Ulam found them “truly amazing”. Fermi told him that he thought they had made a “little discovery”.

The 1955 paper contains an odd footnote: “We thank Ms. Mary Tsingou for efficient coding of the problems and for running the computations on the Los Alamos MANIAC machine.” Mary Tsingou was the underappreciated character in the story. She was a Greek immigrant whose family barely escaped Italy before Mussolini took over. With bachelor’s and master’s degrees in mathematics from Wisconsin and Michigan, in 1955 she was a “computer” at Los Alamos, just like many other women. Her programming of the computer was crucial and non-trivial, but she was acknowledged in the work and not in the writing. She worked later with von Neumann on diffusion problems, was the first FORTRAN programmer, and even did some calculations for Ronald Reagan’s infamous “Star Wars” program. As of 2020, Mary Tsingou is still alive and 92 and living in Los Alamos. The Fermi-Pasta-Ulam problem should be called the Fermi-Pasta-Ulam-Tsingou problem.

Fermi’s sense of having made a “little discovery” has to be one of the great understatements of 20th century physics. The results that he, Ulam, Pasta and Tsingou obtained went beyond harmonic systems and the MANIAC. Until then there had been two revolutions in 20th century physics that changed our view of the universe – the theory of relativity and quantum mechanics. The third revolution was quieter and started with French mathematician Henri Poincare who studied non-linear problems at the beginning of the century. It kicked into high gear in the 1960s and 70s but still evolved under the radar, partly because it spanned several different fields and did not have the flashy reputation that the then-popular fields of cosmology and particle physics had. The field went by several names, including “non-linear dynamics”, but the one we are most familiar with is chaos theory.

As James Gleick who gets the credit for popularizing the field in his 1987 book says, “Where chaos begins, classical science stops.” Classical science was the science of pen and pencil and linear systems. Chaos was the science of computers and non-linear systems. Fermi, Ulam, Pasta and Tsingou’s 1955 paper left little reverberations, but in hindsight it is seminal and signals the beginning of studies of chaotic systems in their most essential form. Not only did it bring non-linear physics which also happens to be the physics of real world problems to the forefront, but it signaled a new way of doing science by computer, a paradigm that is the forerunner of modeling and simulation in fields as varied as climatology, ecology, chemistry and nuclear studies. Gleick does not mention the report in his book, and he begins the story of chaos with Edward Lorenz’s famous meteorology experiment in 1963 where Lorenz discovered the basic characteristic of chaotic systems – acute sensitivity to initial conditions. His work led to the iconic figure of the Lorenz attractor where a system seems to hover in a complicated and yet simple way around one or two basins of attraction. But the 1955 Los Alamos work got there first. Fermi and his colleagues certainly demonstrated the pull of physical systems toward certain favored behavior, but the graphs also showed how dramatically the behavior would change if the coefficients for the quadratic and other non-linear terms were changed. The paper is beautiful. It is beautiful because it is simple.

It is also beautiful because it points to another, potentially profound ramification of the universe that could extend from the non-living to the living. The behavior that the system demonstrated was non-ergodic or quasiergodic. In simple terms, an ergodic system is one which visits all its states given enough time. A non-ergodic system is one which will gravitate toward certain states at the expense of others. This was certainly something Fermi and the others observed. Another system that as far as we know is non-ergodic is biological evolution. It is non-ergodic because of historical contingency which plays a crucial role in natural selection. At least on earth, we know that the human species evolved only once, and so did many other species. In fact the world of butterflies, bats, humans and whales bears some eerie resemblances to the chaotic world of pendulums and vibrating strings. Just like these seemingly simple systems, biological systems demonstrate a bewitching mix of the simple and the complex. Evolution seems to descend on the same body plans for instance, fashioning bilateral symmetry and aerodynamic shapes from the same abstract designs, but it does not produce the final product twice. Given enough time, would evolution be ergodic and visit the same state multiple times? We don’t know the answer to this question, and finding life elsewhere in the universe would certainly shed light on the problem, but the Fermi-Pasta-Ulam-Tsingou problem points to the non-ergodic behavior exhibited by complex systems that arise from simple rules. Biological evolution with its own simple rules of random variation, natural selection and neutral drift may well be a Fermi-Pasta-Ulam-Tsingou problem waiting to be unraveled.

The Los Alamos report was written in 1955, but Enrico Fermi was not one of the actual co-authors because he had tragically died in November 1954, the untimely consequence of stomach cancer. He was still at the height of his powers and would have likely made many other important discoveries compounding his reputation as one of history’s greatest physicists. When he was in the hospital Stan Ulam paid him a visit and came out shaken and in tears, partly because his friend seemed so composed. He later remembered the words Crito said in Plato’s account of the death of Socrates: “That now was the death one of the wisest men known.” Just three years later Ulam’s best friend Johnny von Neumann also passed into history. Von Neumann had already started thinking about applying computers to weather control, but in spite of the great work done by his friends in 1955, he did not realize that chaos might play havoc with the prediction of a system as sensitive to initial conditions as the global climate. It took only seven years before Lorenz found that out. Ulam himself died in 1984 after a long and productive career in physics and mathematics. Just like their vibrating strings, Fermi, Ulam and von Neumann had ascended to the non-ergodic, higher modes of the metaphysical universe.

First posted on 3 Quarks Daily.